Sorry, this entry is only available in Português do Brasil. For the sake of viewer convenience, the content is shown below in the alternative language. You may click the link to switch the active language.
#acessibilidade: imagem do aparelho usado para a ressonância magnética em hospitais.
Texto escrito pelo Prof. Dr. Thiago Branquinho de Queiroz – CCNH/UFABC
O nosso corpo é formado por diferentes moléculas e macromoléculas, como carboidratos, hormônios, aminoácidos, proteínas, entre muitas outras. Também possuímos surpreendentemente bastante água (H2O), em torno de 60%. Todas essas moléculas, por sua vez, são formadas, como sabemos, por átomos e cada átomo é formado por núcleo, que tem carga positiva +Z (esse número é diferente para cada tipo de átomo), e por elétrons que têm carga negativa -Z (na maioria das vezes somos neutros).
Possivelmente, poucas vezes nos damos conta que somos constituídos também por pequenos ímãs, os núcleos, ou melhor, os isótopos (veja, o núcleo é definido pela carga nuclear e o isótopo pela soma de prótons – carga nuclear – e nêutrons). Os elétrons também são “magnéticos”, e fortes, mas, em geral, estes se “blindam” quando associados em moléculas (a exceção são os terríveis radicais livres!).
Muito bem, voltemos aos núcleos/isótopos. O isótopo com maior momento magnético e, portanto, “o ímã mais forte”, é o próton, o núcleo do nosso amigo hidrogênio. Além disso, o próton, 1H, é muitíssimo abundante na Terra (e nos nossos corpos). Vamos aos dados:
1H – Abundância natural (99,98%) – momento magnético (1,5 x 10-3 µβ – µβ, magneton de Bohr, é uma unidade de momento magnético e momento magnético é a quantidade que relaciona quanto o ímã reage ao campo magnético, “a força do ímã”);
2H – (deutério, um nêutron e um próton) – abundância natural (0,02%) – momento magnético (0,46 x 10-3 µβ);
Temos água distribuída em abundância no nosso corpo e ela é composta por oxigênio e hidrogênio. Assim, podemos usar esse monte de átomos hidrogênio como “sonda” de inspeção se tivermos uma tática para identificarmos suas posições interagindo com o seu momento magnético. Essa tática usa o fenômeno da ressonância magnética (nuclear) com diversas técnicas, o que enriquece enormemente as possibilidades de formação de imagens, como veremos adiante. A proposta e o desenvolvimento inicial da ressonância magnética nuclear são devidos aos físicos Isidor Isaac Rabi (1938) [1] e Felix Bloch e Edward Mills Purcell (1946) [2], ambos laureados com Nobel de Física.
Interessante: Devido ao desenvolvimento da energia nuclear (1934), sucedida pela obtenção da bomba nuclear e os terríveis ataques atômicos à Hiroshima e Nagasaki pelos Estados Unidos, já no final da segunda guerra mundial (1945), e acidentes em plantas nucleares, como em Chernobyl (1986), vazamento de Césio 137 em Goiânia-GO (1987), a palavra “nuclear” aterroriza o público geral, pois refere-se ao processo de fissão nuclear que gera enormes quantidades de energia radiante ionizante e térmica.
Já a ressonância magnética nuclear é inofensiva, e refere-se à mudança de orientação dos ímãs dos átomos em campos magnéticos e submetidos à radiofrequência (em frequências similares ao recebido pelo seu radinho de pilha, ou melhor, do sinal do seu celular – provavelmente você não tem um radinho de pilha…). Bom, o fato é que para evitar pânico, normalmente nos hospitais e laboratórios de análises, não está escrito “Imagem por Ressonância Magnética Nuclear (RMN)”, mas somente “Imagem por Ressonância Magnética”.
Mas vamos ao que interessa, como forma-se uma imagem por RMN?
O próton, com momento magnético µP, sob efeito de um campo externo aplicado pelo equipamento (B0), possui dois níveis de energia. Se o momento magnético é alinhado com o campo do equipamento B0, a energia é menor, E- = -½µp B0. Se o alinhamento é antiparalelo, a energia é maior, E+ = +½ µp B0. Quando o “sistema” (o conjunto de ímãs no equipamento) está em equilíbrio térmico, o sistema se encontra em energia menor, E-. O fenômeno de ressonância consiste em fornecer energia ao sistema por aplicação de radiofrequência exatamente igual à energia de transição entre esses dois estados ΔE=µp B0, e assim aumentar a população do sistema em energia maior, E+. O que o equipamento faz a seguir é detectar as transições ΔE entre os estados à medida que o sistema retorna ao equilíbrio, que ocorre enquanto o sistema emite radiofrequência com energia ΔE=µp B0, retornando ao estado de menor energia, E-.
A partir das descobertas da Mecânica Quântica, descobrimos que energia e frequência da onda eletromagnética (f) são diretamente proporcionais (E=hf, em que h é a constante de Planck). Dessa forma, o decaimento do sistema ao equilíbrio é observado como o decaimento da magnetização, que é detectado pela presença de decaimento da radiofrequência emitida pelo sistema (r.f.*). Tecnicamente, o chamamos de decaimento livre da magnetização, e essa é a quantidade física que gera as imagens. O decaimento livre da magnetização é então transformado em “pico de frequência”, por um processo matemático desenvolvido pelo matemático francês Jean-Baptiste Joseph Fourier, a transformada de Fourier (1807). Neste espectro, então, relacionamos a intensidade do sinal à frequência da radiação emitida. A obtenção do espectro de RMN é ilustrada na Figura 1.
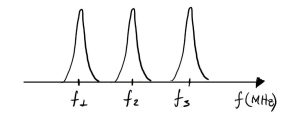
Figura 1: a) O conjunto de ímãs sob efeito de um campo magnético externo B0 e submetido à um pulso de radiofrequência (r.f.) com energia apropriada para inversão do momento magnético dos núcleos (ΔE=µp B0), e portanto frequência f=E/h=µp B0/h; b) Após a inversão de população, o sistema retorna ao equilíbrio “lentamente” emitindo radiação na frequência natural do sistema (r.f.*), característica de cada molécula; A emissão da radiação é observada pelo detector (abaixo à esquerda) e é feita uma transformação matemática para descrever a quantidade de sinal que é emitido naquela frequência (abaixo à direita). A Transformada de Fourier do decaimento da magnetização é o que chamamos de espectro de RMN.
O próximo passo para entendermos como são constituídas as imagens por RMN é relativamente simples. A água e outras moléculas vão gerar espectros de prótons em frequências bem específicas. Isso depende da densidade eletrônica que “blinda” o próton, o que por sua vez depende da natureza das ligações químicas. Além disso, a frequência de emissão do sistema será diretamente proporcional ao campo magnético externo B0. Para ilustrar, façamos agora três experimentos em um único espectro, com campos externos distintos B1 < B2 < B3, aplicados sobre um tubinho de água. O espectro resultante é ilustrado na Figura 2, abaixo. Vemos que, como f=µp B0/h, da mesma forma como B1 < B2 < B3, é também f1 < f2 < f3.
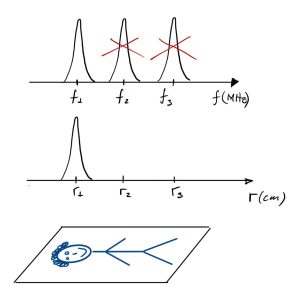
Figura 2: Ilustração de um espectro de RMN do próton da água, por exemplo, obtido com a amostra sob campos magnéticos externos em ordem crescente B1 < B2 < B3, em que f1=µP B1/h e assim sucessivamente.
Para obtermos as imagens, ao invés de fazermos três experimentos, impõe-se que o campo magnético varie de acordo com a extensão do corpo no equipamento. Portanto, sabendo-se como o campo magnético externo varia em função da distância, r, podemos obter espectros em função da frequência e reconstruir um “espectro” em função de r, formando assim a imagem. Por exemplo, observe o Sr. Palito no equipamento de imagem por RMN na Figura 3. O equipamento controla a mudança do campo magnético, de modo que podemos atribuir uma função B(r), por exemplo, B=Axr, onde A é uma constante positiva determinada pelo equipamento. Considerando-se que o Sr. Palito tem água somente na cabeça, onde o campo magnético é dado por B1, somente em f1 o espectro acusará a presença de água. E como sabemos onde está a posição de B3(r3), B2(r2) e B1(r1), sabemos que a cabeça do Sr. Palito está em r1.
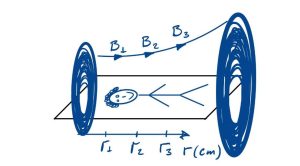
Figura 3: Sr. Palito em um equipamento de imagem por RMN. Note as bobinas laterais atribuindo diferentes intensidades de campo magnético na extensão do corpo do Sr. Palito, representados por B1, B2 e B3.
A conversão final do espectro em imagem é ilustrada na Figura 4. Consideremos que o campo magnético varia com a função B =Axr, onde A é uma constante qualquer positiva. Observamos somente o espectro em f1. Portanto, somente em r1 detectamos água no corpo do Sr. Palito. A conversão de frequência para imagem é simples: f1= µp B1(r1)/h= µp Axr1 / h, de modo que r1=f1.h/µp A. Sendo assim, podemos determinar exatamente onde está a maior concentração de água do Sr. Palito, que é, neste caso, na cabeça.
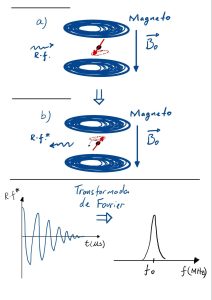
Figura 4: Ilustração da conversão do espectro de RMN em imagem do Sr. Palito.
Na prática, as técnicas para a formação de imagens por RMN são muito mais sofisticadas. O desenvolvimento experimental permitiu obtermos altíssima resolução (muito mais que 3 pontos de B(r)). Também se utilizam medidas em função do tempo de relaxação da magnetização, que é o tempo de retorno do sistema ao equilíbrio, o que eleva o contraste entre áreas ricas em prótons com áreas pobres. Esse é um campo atual e fascinante de desenvolvimento científico e tecnológico multidisciplinar, incluindo-se físicos, químicos, matemáticos e “bio-cientistas” das mais variadas áreas.
Fontes:
[1] Rabi, I.I.; Zacharias, J.R.; Millman, S. & Kusch, P. (1938). “A New Method of Measuring Nuclear Magnetic Moment”. Physical Review. 53 (4): 318–327. https://doi.org/10.1103/PhysRev.53.318
[2] Filler, Aaron (2009). “The History, Development and Impact of Computed Imaging in Neurological Diagnosis and Neurosurgery: CT, MRI, and DTI”. Nature Precedings. https://doi.org/10.1038/npre.2009.3267.5
