#acessibilidade: A imagem é uma ilustração do livro Encontro com Rama, de Arthur C. Clarke. Em tons de azul, vemos o interior da nave Rama, com sua geometria espacial peculiar que nos lembra o interior de uma garrafa – da ótica de uma formiga.
Texto escrito por Eduardo Leme
Você já deve ter se deparado com o falso debate sobre a possível não-esfericidade de planetas. Mas e se eu disser que Arthur C. Clarke escreveu exatamente sobre isso? Nesse texto vamos falar um pouco sobre a nossa percepção sobre alienígenas e geometria.
Em seu livro “Encontro com Rama”, o autor de ficção científica narra a chegada de um estranho asteroide cilíndrico ao nosso sistema solar. Dada sua natureza incomum, uma equipe de astronautas é enviada para investigar o então batizado Rama. Em sua expedição, a equipe da nave Endeavour acaba descobrindo que na verdade Rama é uma espécie de arca alienígena, uma presumida tumba repleta de mistérios.
Para além das discussões filosóficas levantadas pelo autor – como a atemporal “Estamos sozinhos no universo?” – a descrição de Rama é outro ponto da narrativa que merece destaque. O imaginário do extraterrestre humanóide sempre me decepcionou. Me parece preguiçoso imaginar que a evolução da vida inteligente em outra galáxia também culminaria na nossa aparente simetria bilateral bípede. O mesmo raciocínio serve para os meios de transporte. Qual a graça de fantasiar com um OVNI que dá seta?
Quero dizer, por que deveríamos acreditar que entenderíamos, num nível cognitivo, uma outra forma de vida inteligente? Clarke coloca essa pergunta na estrutura de Rama: uma nave cilíndrica totalmente habitável, quase como um planeta móvel.
Estamos acostumados – ou deveríamos – a compreender o planeta como sendo composto por infinitos espaços planos (curvatura espacial nula) que descrevem uma geometria elíptica/esférica (curvatura espacial positiva) quando observados em sua totalidade. Mas no outro extremo da geometria não-euclidiana, encontramos a geometria hiperbólica (curvatura espacial negativa), que descreve o interior da nave. É como se os astronautas da história fossem formigas andando dentro de uma garrafa PET.
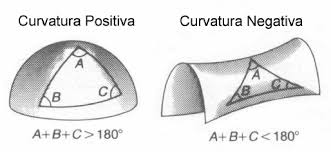
#acessibilidade: A ilustração conta com dois objetos não-euclidianos. À esquerda, uma semiesfera com um triângulo desenhado. Abaixo dela, a soma dos ângulos desse triângulo, que têm resultado maior que 180º. À direita, uma paraboloide hiperbólico, também com um triângulo desenhado. Abaixo dele, a soma dos ângulos desse triângulo, que têm resultado menor que 180º.
A ideia de um habitat espacial cilíndrico pode ter sido popularizada por Clarke, mas não é criação sua. Alguns anos antes da publicação de “Encontro com Rama”, por exemplo, uma proposta desse tipo recebeu bastante destaque em 1974, quando Gerard K. O’Neill, professor de física na Universidade de Princeton, publicou seu “projeto” num artigo da revista Physics Today. O cilindro de O’Neill contaria com gravidade artificial, gerada por sua rotação, e luz solar, fornecida por espelhos contidos em sua extensão, uma atmosfera interna e um anel agrícola.
Tom McKendree também propôs um tipo de cilindro habitável, que abusaria de nanotubos de carbono, numa conferência da NASA em 2000. Seu projeto teria mais de 63 milhões de quilômetros quadrados habitáveis – mais do que a união territorial entre a Europa e a Ásia.

#acessibilidade: A ilustração imagina um par de cilindros de O’Neill. Imagine uma roda conectada a um lado cilindro pelo eixo, e do outro lado, espelhos com uma ponta conectada ao cilindro e a outra livre, deixando-os voltados para o cilindro.
Um último exemplo, esse provavelmente mais famoso, pode ser visto no final de Interestelar (2014). A Estação Cooper, na órbita de Saturno e próxima da ponte Einstein-Rosen do filme – o buraco de minhoca – é também um planetóide desse tipo.
A possibilidade – e as dificuldades – do tráfego espacial nas dimensões e com as capacidades mencionadas ficam para outro post. Fica aqui a recomendação do livro, apesar do pequeno spoiler sobre a natureza de Rama.
Fontes:
Fonte da imagem destacada: Arte de capa da 2ª Edição da Ballantine Books
Figura 1: CRUZ & SANTOS, 2010
Figura 2: Space Colony Art from the 1970s, NASA Ames Research Center. Disponível em: https://nss.org/settlement/nasa/70sArtHiRes/70sArt/art.html