#acessibilidade: Imagem representativa simplificada do sistema Sol-Terra, onde o Sol apresenta-se no centro em relação a Terra, apresentando pontos de estabilidade na orbita. Num fundo preto, uma órbita é desenhada ao torno do Sol, com a Terra nela posicionada e 5 pontos destacados em vermelho estão espalhados conforme o modelo do texto.
Texto escrito pelo colaborador Igor Ribeiro
Se você se interessa por assuntos científicos e acompanha as publicações do Guia dos Entusiastas da Ciência, deve ter visto que já abordamos anteriormente temas que tangenciam as dificuldades de encontrar órbitas estáveis entre três ou mais corpos celestes. Lembra do artigo sobre a série ficcional “O Problema de Três Corpos” ou do texto que explorou as proezas do Telescópio James Webb? (Se não, siga os links no final do texto!) Hoje, continuando nessa linha, vamos nos aprofundar nos pontos lagrangianos, aqueles lugares específicos no espaço onde o próximo objeto que você lançará ao cosmos pode estacionar confortavelmente ou pelo menos, quase confortavelmente.
Por volta de 1750, Leonhard Euler se debruçou sobre as aplicações práticas para determinar pontos estáveis em sistemas de múltiplos corpos. Seus esforços identificaram três pontos (L1, L2 e L3) onde um corpo de pequena gravidade pode permanecer em equilíbrio sob a influência de dois corpos maiores. Algum tempo depois, Joseph-Louis Lagrange continuou essa linha de pensamento e encontrou mais dois pontos (L4 e L5). Estes últimos são conhecidos como os mais “convidativos”, mas chegaremos lá.
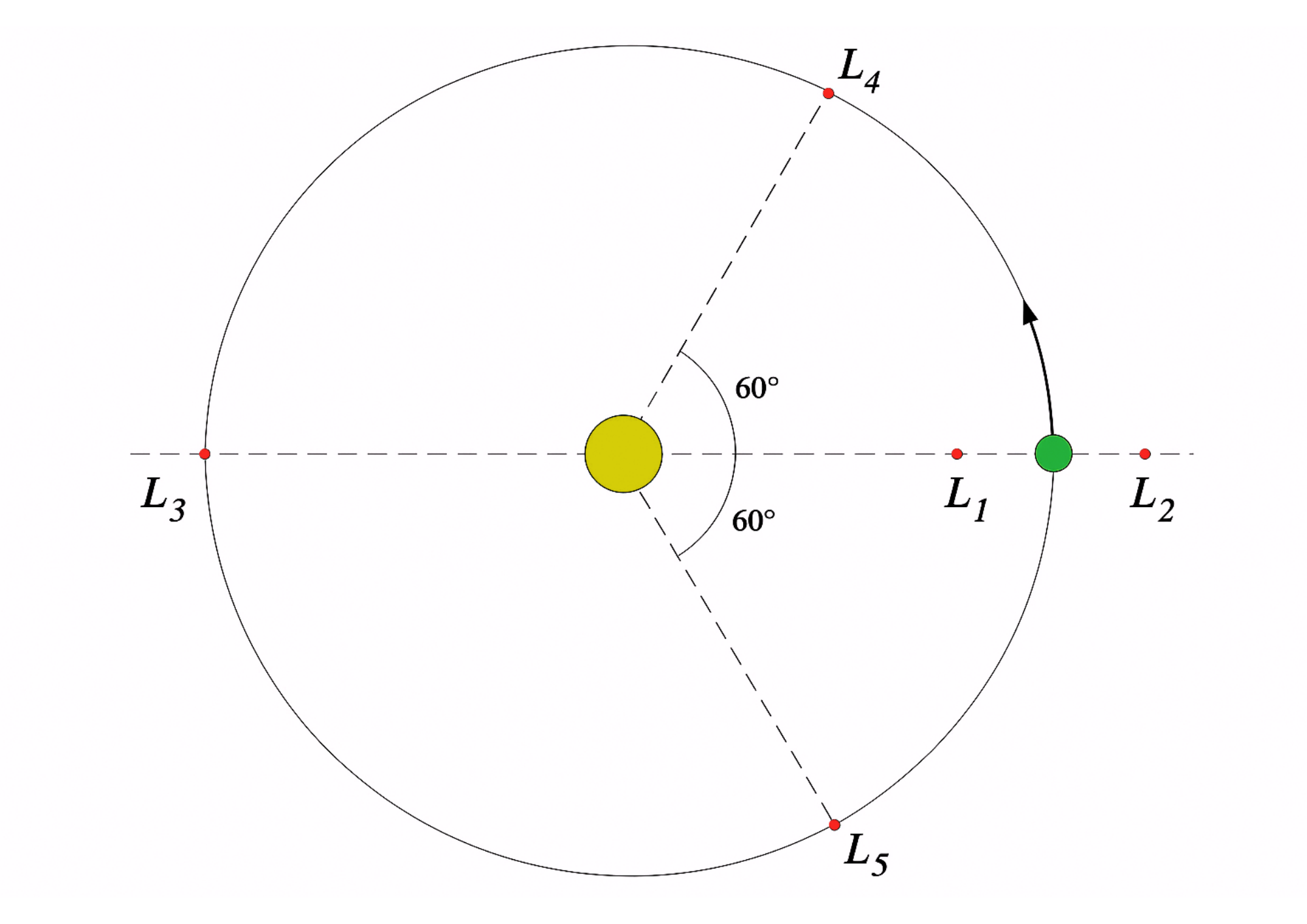
Para facilitar, vamos iniciar imaginando um exemplo clássico: o Sol como o primeiro corpo de maior gravidade, a Terra como o segundo e o objeto que você planeja lançar, como o terceiro.
Se sua missão é monitorar o Sol, L1 é o lugar ideal. Este ponto fica entre o Sol e a Terra, permitindo uma visão ininterrupta de nossa estrela. É onde o Solar and Heliospheric Observatory (SOHO) está posicionado, fornecendo dados cruciais sobre o comportamento do Sol. Por que isso é importante? Porque o Sol não é tão tranquilo quanto parece. Tempestades solares podem causar danos a satélites, interferir em sistemas de comunicação e comprometer viagens espaciais. Ter um observatório estrategicamente posicionado em L1 nos dá uma vantagem: prever e mitigar esses eventos.
Agora, se uma estrela como o Sol é muito banal para você, talvez seja hora de pensar no L2. Este ponto fica à sombra da Terra em relação ao Sol, proporcionando um ambiente extremamente estável e ideal para observações astronômicas. Foi justamente por isso que o Telescópio James Webb escolheu este endereço. No L2, ele pode apontar para a vastidão do cosmos, registrando galáxias distantes e talvez, quem sabe o seu objeto, possa ser o primeiro a registrar diretamente um buraco de minhoca, uma ponte teórica entre diferentes pontos do espaço-tempo, um fenômeno ainda no reino das hipóteses.
Para quem deseja expandir os horizontes, vamos sair do sistema Sol-Terra e imaginar um sistema de tamanho proporcional a suas ambições. Os pontos L4 e L5 do sistema Sol-Júpiter são opções fascinantes. Esses pontos abrigam os asteroides troianos, corpos celestes que compartilham a órbita de Júpiter ao redor do Sol. Eles são como arquivos vivos da formação do Sistema Solar, contendo pistas sobre os blocos de construção da vida. Estudá-los pode revelar como os elementos químicos essenciais chegaram à Terra.
O que torna esses pontos ainda mais especiais é sua estabilidade gravitacional. Localizados a 60 graus à frente (L4) e atrás (L5) de Júpiter, esses pontos estão em um equilíbrio dinâmico perfeito, onde as forças gravitacionais do Sol e de Júpiter se equilibram de forma única. Essa configuração cria uma região de estabilidade gravitacional, permitindo que objetos como os asteroides troianos permaneçam em suas posições por milhões ou até bilhões de anos sem grandes perturbações. Essa estabilidade é crucial, pois sem ela, muitos desses asteroides poderiam ser desviados de suas órbitas e, em alguns casos, até se aproximar da Terra. Graças a esse equilíbrio gravitacional, no entanto, os asteroides troianos ficam protegidos em suas órbitas, longe de riscos de colisões com nosso planeta. Isso torna L4 e L5 locais ideais para observações científicas e missões espaciais de longo prazo.
Tão distante, mas não menos importante, precisamos falar sobre o ponto L3, que no sistema Sol-Terra fica no lado oposto ao Sol em relação à Terra. Este é o lugar para os aventureiros. No entanto, ele vem com uma advertência: é o ponto menos estável entre seus irmãos (L1, L2, L4 e L5), onde pequenas perturbações gravitacionais podem desviar seu objeto. Além disso, como está sempre oculto atrás do Sol, não é possível monitorá-lo diretamente da Terra. Talvez seja por isso que nenhum objeto se encontra por lá ainda.
Escolher um ponto lagrangiano para posicionar seu próximo objeto espacial não é tão simples quanto parece, mas agora você está equipado com parte do conhecimento necessário para tomar essa decisão. Se você prefere estabilidade, escolha L4 ou L5. Para observações inovadoras, L2 é sua opção. Quer desafiar os limites? L3 é para você. E, seja qual for sua escolha, não esqueça de programar seu objeto para enviar dados regularmente. Com tantas descobertas, é bom lembrar que, às vezes, a maior missão que podemos ter é compartilhar o que aprendemos.
Fontes:
CURTIS, Howard D. Orbital Mechanics for Engineering Students. 2nd Edition, Elsevier Ltd., Amsterdam. 2009
SCHAUB, Hanspeter; JUNKINS, John L. Analytical Mechanics of Space Systems. 4. ed. Reston: American Institute of Aeronautics and Astronautics (AIAA), 2021.
GOMES, Tales Augusto Oliveira. Estudo de soluções de buraco negro e buraco de minhoca na teoria de Einstein-Maxwell na presença de campo escalar. 2023. Dissertação (Mestrado em Física) – Universidade Federal do Espírito Santo, Centro de Ciências Exatas, Vitória, 2023
Para saber mais:
E se a gente tivesse três sóis?
Telescópio James Webb, um breve resumo das suas características e principais linhas de pesquisa
Outros divulgadores:
Ciência Todo Dia, YouTube


