#acessibilidade: A imagem é de uma máquina de escrever acinzentada colocada sobre um chão de madeira.
Texto pelo colaborador Matheus Souza Zanzin
Você sabe como um computador funciona? Talvez já tenha ouvido falar que computadores são apenas calculadoras impressionantes que usam somente 0s e 1s, mas qual a teoria por trás disso?
Alan Turing (1912-1954), cujo nome você pode conhecer, propôs o conceito de uma máquina automática (a-machine), que eventualmente ficou conhecida como máquina de Turing. Implementações deste modelo teórico são o que hoje conhecemos como “computadores”. Para entender o que é uma máquina de Turing, vamos entender o modo que seu modelo foi desenvolvido, com base em abstrações sobre máquinas de escrever.
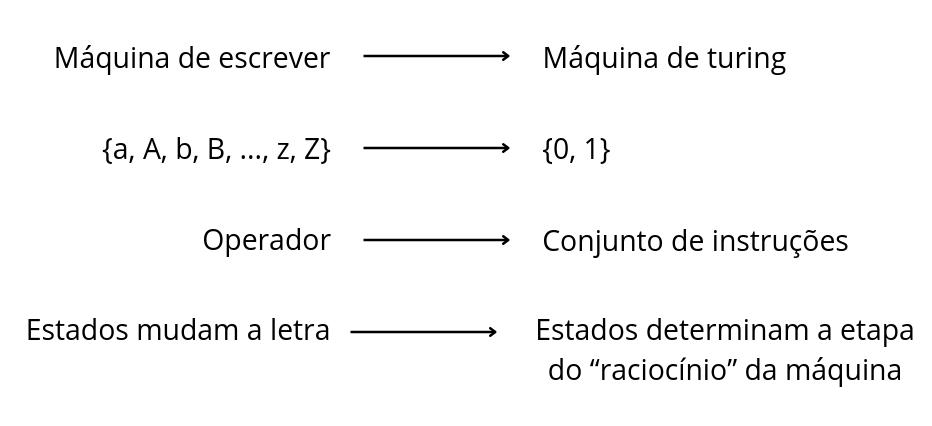
Primeiramente, vamos defini-las: uma máquina de escrever é apenas um equipamento que escreve símbolos, com os símbolos sendo o alfabeto. Ao apertar uma tecla do teclado, a máquina escreve uma letra minúscula ou maiúscula, dependendo da tecla shift ter sido ou não pressionada. Em outras palavras, a tecla shift muda o comportamento da máquina – o símbolo que será escrito – de letras minúsculas para maiúsculas. Essa alteração no comportamento da máquina reflete o que chamaremos por enquanto de “estados”. Após escrever um símbolo, a máquina move o papel para escrever o próximo símbolo ao lado do que foi escrito por último. Repare que, para que a máquina de escrever funcione, é necessário, além do papel, um operador que manipule os estados e decida quais símbolos devem ser escritos, sua ordem, e quando é necessário trocar de linha por ter acabado com o espaço no papel.
Mas e se fosse diferente? Como poderíamos remover o operador? Essa pergunta nos leva à máquina de Turing, que seguindo instruções previamente definidas, torna-se independente de um operador humano.
As abstrações necessárias para isso são as seguintes: o papel da máquina de escrever é substituído por uma fita, esta sendo infinita e dividida em quadrados que podem conter símbolos como 0 e 1 ou um espaço em branco. Uma “cabeça” de leitura e escrita atua como o conjunto de teclas da máquina de escrever, mas ao invés de ser controlada por um operador, ela automaticamente lê o símbolo presente, decide o que fazer com base no estado atual da máquina, e executa a ação. A ação pode ser: sobrescrever o símbolo (isto é, apagar o que está no quadradinho e escrever outra coisa), mover a cabeça para a esquerda ou para a direita, e entrar em um novo estado. Tudo isso é controlado por regras de transição, que nada mais são do que uma sequência de instruções bem definidas.
Com isso em mente, falta ainda entender o que são os estados na máquina de Turing. Em nossa máquina de escrever, são os modos de escrita: quando o shift está pressionado, a máquina de escrever entra em um estado em que a tecla “a” imprime um “A” maiúsculo. Entretanto, na máquina de Turing, estados – como q0, q1 e q2 – indicam em que parte do “raciocínio” a máquina está. Dependendo do estado atual e do símbolo lido na fita, a máquina segue uma regra de transição que determina como continuar o processo.
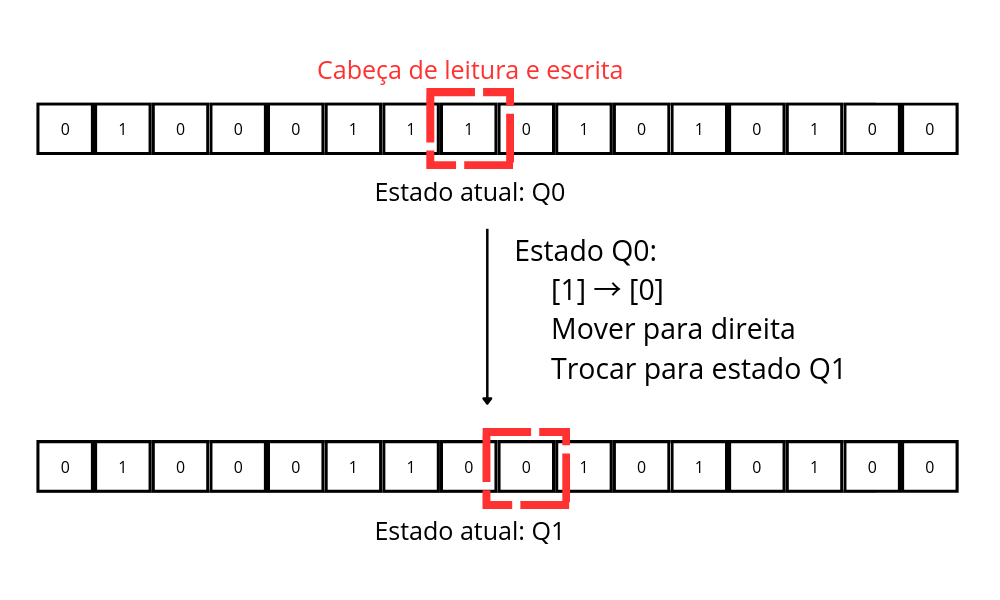
Por exemplo, imagine uma regra de transição que diz: se a máquina está no estado q0 e lê o símbolo “1”, ela deve apagar esse “1” e escrever um “0” em seu lugar, mover a cabeça uma posição para a direita e mudar seu estado para q1 – caso tenha ficado muito abstrato, a imagem abaixo demonstra este exemplo de forma visual (Figura 2). Traçando um paralelo com a máquina de escrever, isso é o equivalente a estar no “modo maiúsculas” (ou seja, a tecla shift está apertada) e decidir que, ao apertar “a”, a máquina escreverá “A” e passará para o próximo caractere da linha. Tendo em mente esta noção de estado, temos finalmente uma versão simplificada e próxima da definição formal da máquina de Turing. O elemento que difere a nossa máquina de uma máquina de Turing definida formalmente será abordado no fim do texto, mas para compreender o funcionamento da máquina, a versão simplificada basta.
Com o mecanismo descrito, Turing demonstrou que é possível construir algoritmos inteiros apenas com fita, símbolos e um conjunto de regras baseadas em estados. Vamos agora a um exemplo prático e mais completo: detectar se uma sequência de símbolos 0 e 1 possui um número par de 1s. Nesse caso, queremos que a máquina leia a fita (como se fosse uma linha de texto) e nos diga se o número de 1s encontrados é par. Para isso, vamos precisar de dois estados: P e I, com P significando que o número de 1s encontrado até o momento é par, e I significando que é ímpar.
A máquina em nosso exemplo começa no estado P, pois se ela ainda não leu nenhum número, o número de 1s lidos é 0, e 0 é par. Ao percorrer a lista, toda vez que encontra um 1, a máquina muda de estado (se o estado era P, vira I. Se estava em I, vira P). Ao terminar de ler a sequência, basta verificar o estado em que a máquina parou. Se o estado for P, a sequência tem um número par de 1s, e se for I, um número ímpar. Repare que, neste exemplo, verificamos a paridade de 1s sem precisar contar a quantidade de 1s, apenas alternamos entre dois estados. Há diversos casos como este, nos quais a máquina de Turing consegue “contar” sem usar números.
Existem, no entanto, problemas que fazem com que a máquina precise contar, e a forma que ela faz isso é, em uma palavra, elegante. A máquina de Turing, mesmo tão simples quanto a definimos, é capaz de “simular” álgebra, e ainda por cima, consegue fazê-lo em múltiplos sistemas de contagem, tudo a depender da modelagem feita nos estados e nas regras de transição! Para demonstrar isso, façamos do último exemplo deste texto uma conta simples: 2 + 3 = 5.
A máquina de Turing – e, por consequência, a versão simplificada que definimos – não consegue armazenar valores, e essa é a maior dificuldade com a qual precisaremos lidar em nossa conta. Uma forma de contornar isso é representar os valores dos números como repetição de símbolos, de forma que 2 se torne 11 ou 00, 3 se torne 111 ou 000, etc. O que importa é que os símbolos se repitam.
Esta lógica de repetição é o método que adotaremos para resolver a nossa conta da primeira forma, adotando 1 como o símbolo a ser repetido, resultando em: 11 + 111 = 11111. Para a conta, precisaremos de um separador na fita entre 11 (que representa 2) e 111 (que representa 3), e para este separador, usaremos o 0. Precisaremos também das regras de transição e dos estados de nossa máquina. A ideia central deste método é unir ambos os lados separados pelo 0, e ao encontrarmos um espaço em branco, terminamos a nossa conta. Para isso, definimos os seguintes estados e regras de transição:
– q0 (o estado inicial): enquanto a máquina ler 1, ela se moverá um quadradinho para a direita. Ao ler 0, move-se um quadradinho para a direita e troca para o estado q1. Se ler um quadradinho em branco na fita, acaba com a operação da soma e encerra o algoritmo.
– q1: quando lê 1, sobrescreve-o por 0, e move uma casa para a esquerda. Quando lê 0, sobrescreve-o com 1, move uma casa para a direita e muda para o estado q0.
O resultado desta modelagem é:
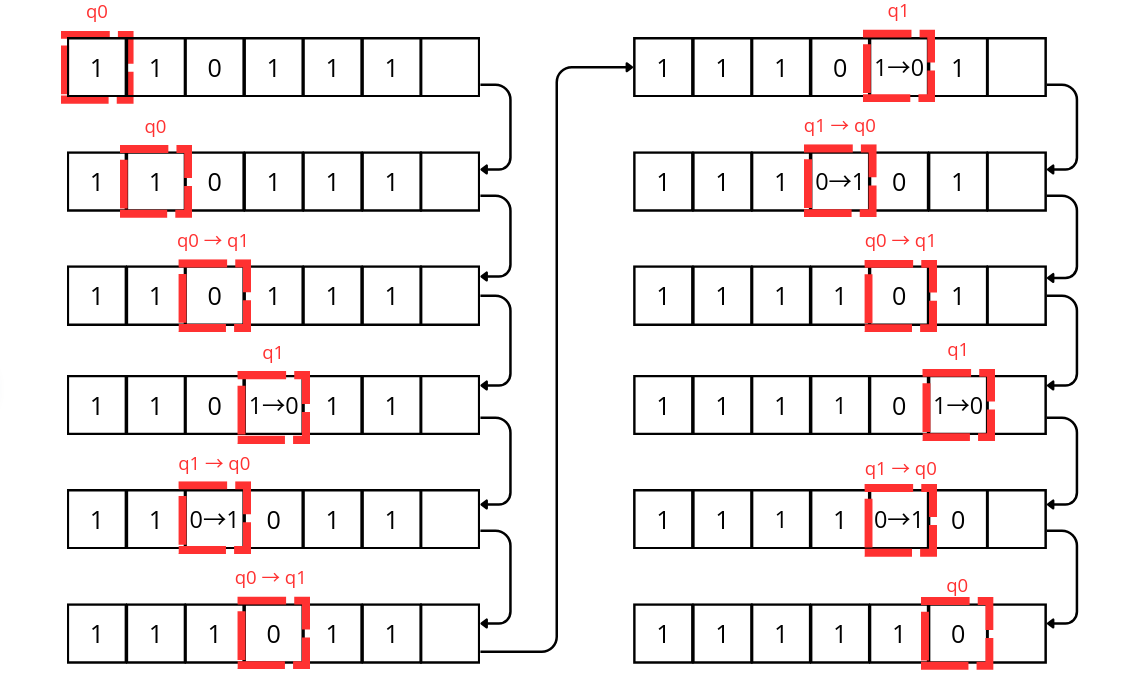
Ao final, a máquina está no estado q0, movendo-se para um quadradinho em branco, que encerrará a sua execução. Mais importante, o valor da sequência de 1s que obtivemos foi 11111, que, na forma que modelamos, equivale a 5, resultado correto da nossa equação (2 + 3 = 5).
Essa é apenas uma forma de modelar a aritmética em uma máquina de Turing. Outra maneira seria utilizando base binária (2 = 10, 3 = 11, 5 = 101), que é como os computadores funcionam. (É assim máquinas de Turing modelem computadores!) Porém, para utilizar álgebra em base binária, seria necessário o único elemento presente na máquina de Turing que não está presente na máquina simplificada que utilizamos nos exemplos até agora: um segundo conjunto de símbolos, mas, dessa vez, temporários. Vale avisar a você, Entusiasta, que a partir deste momento, pode ser necessário possuir algum conhecimento básico de operações em sistemas binários. Caso não o possua, recomendo a curta sessão sobre adição neste site: https://embarcados.com.br/operacoes-com-sistemas-binarios/.
O motivo para precisarmos de símbolos temporários é simples: tente encontrar uma forma de organizar os números que somaremos em nossa fita, de forma que eles fiquem separados. É imprático – para não dizer impossível – utilizar 0 como separador, pois 0 é uma parte integral da base binária, e seu uso tornaria impossível diferenciar entre o separador de dois números e um número binário maior. Por exemplo: a soma 2 + 3, em binário é o mesmo que 10 + 11, que deveria ser 101, porém, fazer isso usando 0 como separador resulta, em nossa fita, na sequência 10011, que equivale ao número 19. Como diferenciar, então, 2+3 de 19?
Você pode tentar encontrar outra solução que não utilize ativamente espaços em branco como separadores, porém toda operação binária, independentemente de utilizar 0 ou 1 como separador, ocasionará no problema de indistinguibilidade entre os dois números com um separador binário e um número binário que não é o resultado da soma.
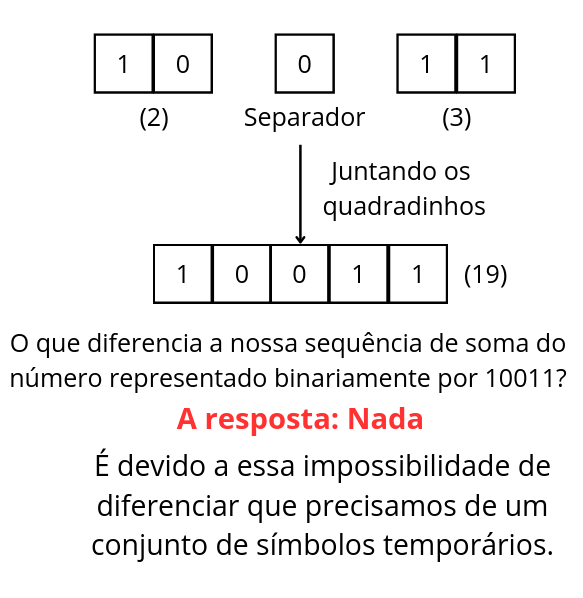
Agora que sabemos que não é possível modelar os separadores de forma binária, temos a necessidade de implementar símbolos temporários em nossa máquina. Com isso, chega o momento de transformarmos o nosso modelo básico – que criamos neste texto a partir de abstrações de uma máquina de escrever – em uma verdadeira máquina de Turing. Os símbolos temporários servem como marcas temporárias, que não fazem parte da sequência de entrada da fita e nem da sequência resultante, mas que nos permitem lidar com limitações que surgem devido à modelagem com 0s e 1s. Desta forma, podemos utilizar um símbolo para marcar onde cada número termina. Chamemos este separador de s, como resultado, a nossa fita agora deixa de ser 10011 e se torna:
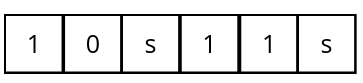
Assim, temos agora uma enorme variedade de formas para modelar nossa soma, contanto que as marcações temporárias sejam removidas, eventualmente, de modo que a sequência que reste na fita seja composta apenas por 0s e 1s. Agora, basta criar os estados e as regras de transição para que a nossa máquina consiga somar quaisquer valores binários. Mas por que parar apenas na soma? É possível utilizar outros separadores, letras diferentes de nosso conjunto de símbolos temporários, cada uma denotando uma operação – como por exemplo: Separadores = {“+”, “-”, “x”, “/” }. Desde que a quantidade de estados e regras de transição aumente de forma a conseguir administrar todos eles, é perfeitamente possível criar uma máquina de Turing que consiga fazer todas as operações.
Na verdade, não apenas é possível, como já foi feito. Existem diferenças entre o modelo teórico e a prática, de fato, mas computadores são, afinal, máquinas de Turing! Ou, pelo menos, são modelados por elas. No lugar de símbolos temporários, computadores utilizam circuitos lógicos para identificar e realizar suas operações matemáticas; no lugar de 0s e 1s, eles usam a energia elétrica percorrendo os circuitos, com 0 sendo equivalente a um circuito desligado, e 1 a um circuito ligado, a cabeça de leitura e escrita se tornando uma CPU, e assim por diante.
Detalhes mudam, mas a visão geral é uma só: computadores foram criados a partir do modelo da máquina de Turing. Essa torna-se então um testamento matemático de que complexidade pode ser resolvida com simplicidade, pois, simples como ela é, abstraída dos elementos mais básicos e crús de uma máquina de escrever, e contando com um alfabeto fixo constituído por meros dois símbolos, ela baseia todo o comportamento lógico e abstrato das máquinas mais complexas e consolida, possivelmente, o uso mais difundido dentre todas as invenções tecnológicas.
Fontes:
Artigo no qual Turing descreveu sua máquina. https://londmathsoc.onlinelibrary.wiley.com/doi/epdf/10.1112/plms/s2-42.1.230
Boy Who Wanted to ‘Make a Typewriter’ Instead Became Father of Computer Science
Imagem destacada: https://pt.wikipedia.org/wiki/Ficheiro:Olivetti_Lettera_22_by_LjL.jpeg
Para saber mais:
Artigo que explica operações binárias https://embarcados.com.br/operacoes-com-sistemas-binarios/
O que tem a ver um tear com a era dos computadores?
Ada Lovelace e os números de Bernoulli
Outros divulgadores:
Caso queira
- desenvolver na prática uma noção de como computadores usam circuitos eletrônicos e onde diferem das máquinas de Turing, recomendo o jogo: https://store.steampowered.com/app/1444480/Turing_Complete/
- um vídeo mais técnico com uma breve explicação histórica e que aborda temas além deste artigo: https://www.youtube.com/watch?v=G4MvFT8TGII
- um vídeo mais simples e curto que também explique o que é uma máquina de turing: https://www.youtube.com/watch?v=dNRDvLACg5Q


