#acessibilidade: A imagem contém um diagrama de Euler-Venn, contendo os conjuntos P, NP e NP-Difícil. P é subconjunto de NP, e a intersecção entre NP e NP-Difícil é denominada “NP-Completo”.
Texto escrito pelo colaborador Matheus Souza Zanzin
O título chamou atenção e você está aí pensando em quais, dentre tantos possíveis, seriam os sete problemas do milênio? De fato, adivinhar os principais problemas do futuro da humanidade não é uma tarefa fácil. Por isso, este artigo marca o começo de uma série de artigos que dissertam sobre esses problemas. Nesse texto, você vai conhecer um dentre os sete: o problema P vs. NP. Ainda sem solução, ele é considerado o mais importante da ciência da computação. Ele une as mais diversas áreas da matemática, tanto pura como aplicada, abrangendo áreas como a teoria de grafos, probabilidade, topologia, álgebra e teoria dos números, revelando conexões não-triviais entre elas.
Formalizado em 1971 e advindo do campo da complexidade computacional, que é o ramo da ciência da computação que estuda a eficiência de algoritmos, P vs NP é um problema que é relativamente simples de entender conceitualmente. Mas antes de entender o problema, é necessário saber o que é um algoritmo e o que são as classes P e NP.
Vamos começar por algoritmos: em termos simples, um algoritmo é um conjunto de instruções que são executadas uma após a outra, como uma receita culinária. Em computadores, essas instruções são codificadas em 0’s e 1’s, isto é, são codificadas no sistema binário, para eventualmente serem executadas pelo computador. Para facilitar a escrita de códigos, foram criadas as linguagens de programação, que são ferramentas que permitem que um algoritmo seja escrito em forma de código em uma linguagem simples, para então ser traduzido para binário. Um exemplo de algoritmo bem simples que será utilizado ao longo do texto é o seguinte código em Python de função exemplo que verifica se os números de uma lista são pares ou ímpares:
def verifica_par(lista_valores):
paridades = []
for valor in lista_valores:
if valor % 2 == 0:
paridades.append(True)
else:
paridades.append(True)
return paridades
lista_teste = [0, 1, 2, 3, 4, 5, 6, 7]
print(verifica_par(lista_teste))
Caso não saiba programar, não se assuste, o código é simples de entender. É criada uma função – na imagem: verifica_par(lista_valores) -, que recebe uma lista de valores numéricos e verifica se eles são pares, e anota o valor da paridade de cada valor em uma outra lista, anotando True (Verdadeiro) caso o número seja par, e False (Falso) caso o número seja ímpar.
Ao executarmos a função com os números inteiros de 0 a 7, a lista de paridade que é criada pela função é composta por valores booleanos (True e False) que alternam entre si, como pode ser visto no vetor abaixo.
[True, False, True, False, True, False, True, False]
Vamos agora expor um pouco da natureza binária do nosso código. Mais especificamente, vamos verificar os valores numéricos de True e False. Isso é feito no código abaixo:
print("O valor numérico de True é: ", int(True))
print("O valor numérico de False é: ", int(False))
Executar este trecho de código resulta em:
O valor numérico de True é: 1
O valor numérico de False é: 0
Isso são valores binários! Isso significa que, por debaixo dos panos, a lista de paridades criada pela função verifica_par é apenas uma lista composta por itens com valores de 0 e 1. Com isso em mente, do ponto de vista matemático, o nosso exemplo pode ser escrito como:
\( verifica\_par([0,1,2,3,4,5,6,7])\to[1,0,1,0,1,0,1,0] \)
É importante lembrar que os valores numéricos da lista de valores que são passados para a função verifica_par também podem ser descritos de forma binária, que é como o computador os processa. Falando da função verifica_par, ela pode ser denotada da seguinte forma:
Seja uma lista de números inteiros \( \mathbf{x} = [x_1,x_2,…,x_n] \). Definimos a função
\( verifica\_par: \mathbb{Z}^{|\mathbf{x}|}\to \{0,1\}^{|\mathbf{x}|}\)
Tal que
$$
\text{verifica_par}(x_i) =
\begin{cases}
1, & \text{se } x_i \text{ for par} \\
0, & \text{se } x_i \text{ for impar}
\end{cases}
$$
A aplicação da função a todos os elementos da lista de entrada gera um vetor binário:
\( \mathbf{y} = [{verifica\_par}(x_1), {verifica\_par}(x_2), …, {verifica\_par}(x_n)] \)
Ou seja, um vetor que indica com 1 os elementos pares e com 0 os ímpares.
Agora que temos uma definição do que é um algoritmo e uma noção básica de como algoritmos podem ser descritos matematicamente, precisamos entender o que são as classes P e NP. Comecemos por P.
A classe P denota um problema que possui uma solução eficiente conhecida, com esta solução estando na forma de um algoritmo. Tenha em mente que “eficiente” neste contexto significa que, no pior dos casos, o algoritmo será executado em tempo polinomial, não importando o quão grande seja o grau do polinômio. O motivo de o tempo polinomial ser considerado eficiente é simples: as funções polinomiais “crescem” (isto é, seus valores aumentam) de forma mais devagar do que funções exponenciais e fatoriais. Você pode se perguntar o quão mais devagar, e para obter uma dimensão dessa diferença, basta olhar o gráfico abaixo.
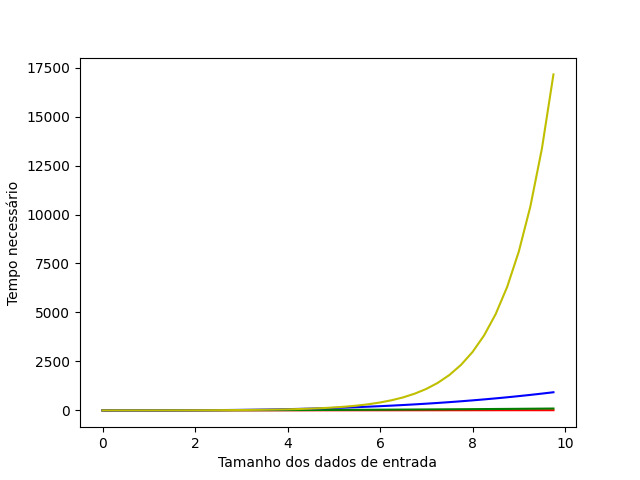
No gráfico, a linha vermelha mostra o tempo necessário para execução de funções com aumento de tempo linear (polinomial de grau 1). A linha verde, com aumento de tempo em ritmo quadrático (polinomial de grau 2). Na linha azul, o aumento de tempo segue ritmo cúbico (grau 3). Por fim, a linha amarela representa funções cujo tempo de execução cresce em ritmo exponencial. Quando visualizado em um gráfico, é fácil entender que o aumento do tempo de execução das funções não-polinomiais é muito maior – e por consequência, muito menos eficiente – do que o das funções polinomiais.
Um exemplo de algoritmo elemento da classe P é o nosso algoritmo da função verifica_par. Se a função precisar verificar a paridade de um único número, ela fará isso em um tempo. Se forem verificados dez números ao invés de um, o tempo necessário será aproximadamente 10 vezes maior, e se forem cem números, o tempo será aproximadamente 100 vezes maior. Em suma, se tivermos n verificações, o tempo será aproximadamente n vezes o tempo de uma única verificação. Isso revela o comportamento linear do tempo de execução da função verifica_par.
Agora vejamos NP, que é a classe mais difícil de compreender conceitualmente. É mais fácil de entender por meio de um exemplo simples, embora um tanto absurdo: O número 3 é primo, assim como o número 2. Já o número 6 é composto, pois é um número que é obtido após multiplicar 3 por 2. Para verificar isso, basta multiplicar 3 e 2. Mas e quanto a um número arbitrário, como o 67º número de Mersenne (isto é, \(2^{67}-1\))? Como verificar se ele é primo ou não? Um algoritmo que descobre se ele é primo (ou não) envolve verificar de forma exaustiva todos os produtos entre números primos conhecidos até encontrar alguma combinação que resulte em \(2^{67}-1\). Embora o algoritmo para descobrir os componentes do número de Mersenne possa não ser eficiente, existe uma verificação eficiente. Basta calcular:
\( 2^{67}-1 = 147573952589676412927 = 193707721 \cdot 761838257287 \)
Essa verificação é eficiente, pois ela consiste apenas em multiplicar dois números, mas ela não leva em conta o tempo necessário para encontrar esta multiplicação dentre todos os outros produtos possíveis entre números primos. Esse exemplo encapsula bem a essência da classe NP: Um problema em NP é um problema cuja solução pode ser verificada de forma eficiente, independentemente do tempo necessário para encontrar a solução em questão. Isso nos leva ao problema do início do artigo: P vs NP.
Conhecendo P e NP, vamos agora a um dos problemas do milênio: P vs. NP. Em outras palavras, seria P igual a NP? Isto é, será que para todo problema que pode ser verificado de forma eficiente, existe um algoritmo que encontra a solução de forma eficiente? A maioria da comunidade acadêmica acredita que não, porém ainda não existe uma única prova ou resolução válida para este problema, e, portanto, ele segue sem solução. E sua importância não pode ser subestimada. Dentre os problemas de NP, está incluída toda a base da criptografia moderna, que protege senhas de bancos e informações privadas na internet. Se P for igual a NP, significa que existe um algoritmo eficiente que pode desvendar cada tipo possível de criptografia. Porém, se P for igual a NP, isso significaria também diversos avanços positivos em áreas como física, matemática, biologia, logística, e toda e qualquer área que precisa lidar com um grande volume de informações que ainda não possui métodos eficientes de fazê-lo.
Mas como resolver P vs. NP? Como provar que cada um dos problemas em NP possui um algoritmo eficiente? Ou como provar que isso é impossível? Provar cada um dos problemas seria impossível, já que contando com as diferentes formas de construir cada problema, o número de elementos em NP é infinito. Para lidar com isso, existem os conceitos de NP-difícil e NP-completo.
De forma resumida, um problema é “NP-difícil” se ele é pelo menos tão difícil quanto todos os outros problemas em NP, possivelmente sendo até mais complexo do que os problemas em NP, caso ele não possua uma verificação conhecida que seja eficiente. Neste sentido, problemas NP-difíceis podem superar problemas NP em complexidade, de forma que diversos problemas que são NP-difíceis não sejam elementos da classe NP.
Existem, no entanto, problemas NP-difíceis que pertencem à classe NP, e para estes problemas, existem funções que permitem transformar todos os problemas em NP em problemas equivalentes, de forma que resolver um único problema dentre estes resultaria em resolver todos os problemas em NP. Problemas que pertencem tanto à classe NP quanto a NP-difícil, e possuem uma tradução/modificação para outros problemas NP são chamados de “NP-completos”. É essa propriedade de tradução entre problemas NP-completos que permite que estes problemas unam diversas áreas da matemática que inicialmente podem parecer não possuir nada em comum, como a álgebra booleana e a teoria de grafos e a topologia.
Caso a ideia de “traduzir” um problema ou um algoritmo pareça difícil, lembre-se da nossa função verifica_par. A tradução mais simples seria seu oposto, uma função que verifica ímpares, chamemos ela de verifica_impar. Para fazer essa tradução, basta seguir o seguinte raciocínio:
Se nós temos uma função que, dada uma lista de valores iniciais, resulta em uma lista de números binários, é possível criar uma função que atua na lista resultante, modificando o resultado, traduzindo a solução de um problema para a solução de outro. No caso de verifica_impar, basta inverter os valores da lista resultante de verifica_par para obter os valores ímpares. Trocando para 1 onde o resultado de verifica_par foi 0, e trocando para 0 onde o resultado foi 1. Matematicamente:
Seja uma lista de valores binários \( \mathbf{x} = [x_1,x_2,…,x_n] \). Com a função verifica_par definida, definimos a função
\( verifica\_impar: \mathbb{Z}^{|\mathbf{x}|}\to \{0,1\}^{|\mathbf{x}|}\)
Tal que
$$
\text{verifica_impar}(x_i) =
\begin{cases}
1, & \text{se } \text{verifica_par}(x_i) = 0 \\
0, & \text{se } \text{verifica_par}(x_i) =1
\end{cases}
$$
A aplicação da função a todos os elementos da lista de entrada resultante de verifica_par gera um vetor binário que é oposto ao vetor de entrada:
\( \mathbf{y} = [{verifica\_impar}(x_1), {verifica\_impar}(x_2), …, {verifica\_impar}(x_n)] \)
Ou seja, um vetor que indica com 0 os elementos pares e com 1 os ímpares.
Com essa transformação de verifica_par para verifica_impar, chegamos finalmente ao fim deste artigo! Você imaginava que um problema que foi descoberto no começo dos anos 70 poderia ser tão importante ao ponto de conectar toda a matemática? E este é apenas um dentre os sete problemas do milênio, com alguns dos outros problemas sendo possivelmente até mais importantes do que o PvsNP! Caso tenha se interessado em saber mais sobre eles, basta esperar, pois em breve eles serão abordados aqui no blog, um por vez, de forma compreensível.
Fontes:
WIDGERSON, Avi. Mathematics and Computation: A Theory Revolutionizing Technology and Science. Princeton University Press, 2019. Disponível em: https://www.math.ias.edu/files/Book-online-Aug0619.pdf
Lista dos problemas do milênio, disponível em https://www.claymath.org/millennium/p-vs-np/
Fonte das imagens usadas ao longo do texto: autoria própria.
Para saber mais:
Caso tenha se interessado pelo assunto, por algum dos exemplos ou pela teoria da complexidade computacional, recomendo fortemente ler o livro utilizado como fonte (está disponível gratuitamente online): Mathematics and Computation, por Avi Widgerson. Disponível em: https://www.math.ias.edu/files/Book-online-Aug0619.pdf
Caso o que tenha te chamado atenção tenha sido a parte sobre a relação entre o tempo de execução de um algoritmo e a quantidade de valores de entrada, a aula sobre big O disponível no site do MIT pode te interessar. Disponível em: https://web.mit.edu/16.070/www/lecture/big_o.pdf
Caso tenha curiosidade sobre o que é um número de mersenne: https://en.wikipedia.org/wiki/Mersenne_prime
Caso queira ver uma aplicação prática de números de mersenne: https://palaiologos.rocks/posts/mersenne-twister/
Outros divulgadores:
O problema de 1 MILHÃO de DÓLARES – Ciência todo dia – https://www.youtube.com/watch?v=9WwYO1Jtr7Y
P vs NP and the Computational Complexity Zoo – Hackersdashery – https://youtu.be/YX40hbAHx3s?si=QqWpyrkek-nYLLxl
Biggest Puzzle in Computer Science: P vs. NP – Quanta Magazine – https://youtu.be/pQsdygaYcE4?si=EW1HS3Nh3HfUbZqw





